Pavel Stránský
Kontakt: Contact
Česky English
Logo
Naposledy aktualizováno: 5.6.2024
κ
2
4
Typ
C=D
S-S (C+D=4)
rigid (C+D=40)
integrable (B=C=0)
asymmetric
asymmetric (C=D=20)
B C D›››
0 0.1 0.10 0.2 0.20 0.3 0.3
0 0.4 0.40 0.5 0.50 0.6 0.6
0 0.7 0.70 0.8 0.80 0.9 0.9
0 1 10 2 20 4 4
0 10 100 20 200 50 50

Dynamika Creaghova-Whelanova potenciálu
Poznámky (pdf)
Termodynamika (pdf)
Geometrická metoda (pdf)
Oscilující část hustoty hladin (pdf)		 Hamiltonián
A=0A=1A=2
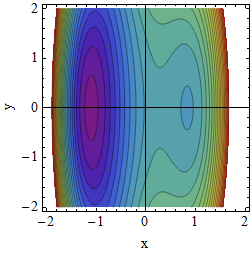Potenciál A=0Potenciál A=1Potenciál A=2
Obrázek 1. Ekvipotenciální plochy (do energie E=2,5).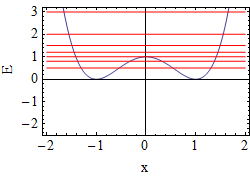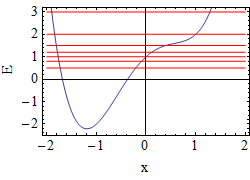
Potenciál y=0, A=0Potenciál y=0, A=1Potenciál y=0, A=2
Obrázek 2. Řez y=0 potenciálem s vyznačenými energiemi pro Poincarého řezy v Obrázku 4 (červeně).
freg
Obrázek 3. (A; E) Klasická regularita freg (bílá-regularita: freg=1, černá-chaos: freg=0).
Zelené čárkované čáry oddělují plně konvexní a částečně konkávní tvar hranice kinematicky dostupné oblasti.
Červené čáry odpovídají polohám stacionárních bodů potenciálu (kritický trojúhelník).
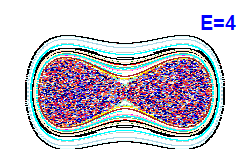
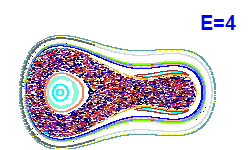
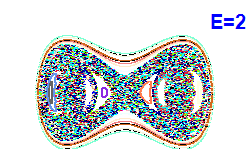
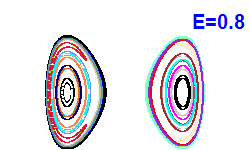
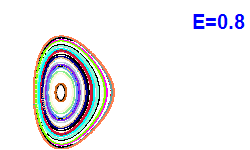
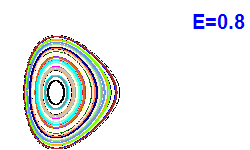
V modrých bodech jsou napočítány Poincarého řezy z Obrázku 4.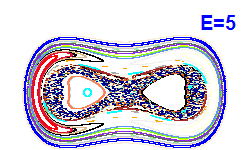
Poincarého řez A=0, E=5Poincarého řez A=1, E=5Poincarého řez A=2, E=5
Poincarého řez A=0, E=4Poincarého řez A=1, E=4Poincarého řez A=2, E=4
Poincarého řez A=0, E=3Poincarého řez A=1, E=3Poincarého řez A=2, E=3
Poincarého řez A=0, E=2Poincarého řez A=1, E=2Poincarého řez A=2, E=2
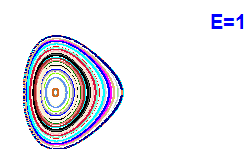Poincarého řez A=0, E=1.5Poincarého řez A=1, E=1.5Poincarého řez A=2, E=1.5
Poincarého řez A=0, E=1.2Poincarého řez A=1, E=1.2Poincarého řez A=2, E=1.2
Poincarého řez A=0, E=1Poincarého řez A=1, E=1Poincarého řez A=2, E=1
Poincarého řez A=0, E=0.8Poincarého řez A=1, E=0.8Poincarého řez A=2, E=0.8
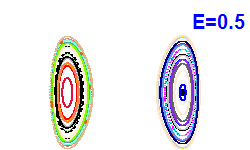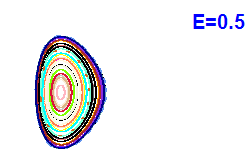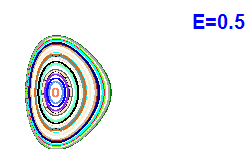Poincarého řez A=0, E=0.5Poincarého řez A=1, E=0.5Poincarého řez A=2, E=0.5
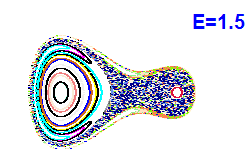
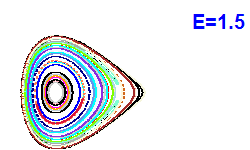
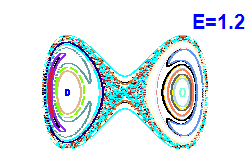
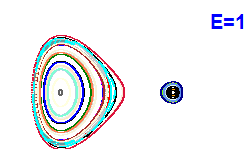
Obrázek 4. Poincarého řezy (x, px; y=0).
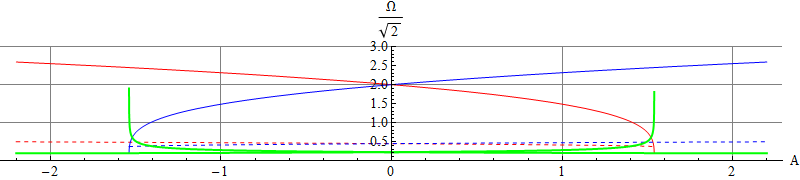Frekvence
Obrázek 5. Frekvence harmonických oscilací v jednotlivých minimech (modře v levém, červeně v pravém), plná čára ve směru x, čárkovaná čára ve směru y. Zelené silné čáry znázorňují poměr frekvencí y:x (rigidity ratio) v obou minimech.
hbar=0.2
Dynamika hladin hbar=0.2Peresova mříž <x> hbar=0.2
hbar=0.1
Dynamika hladin hbar=0.1Peresova mříž <x> hbar=0.1
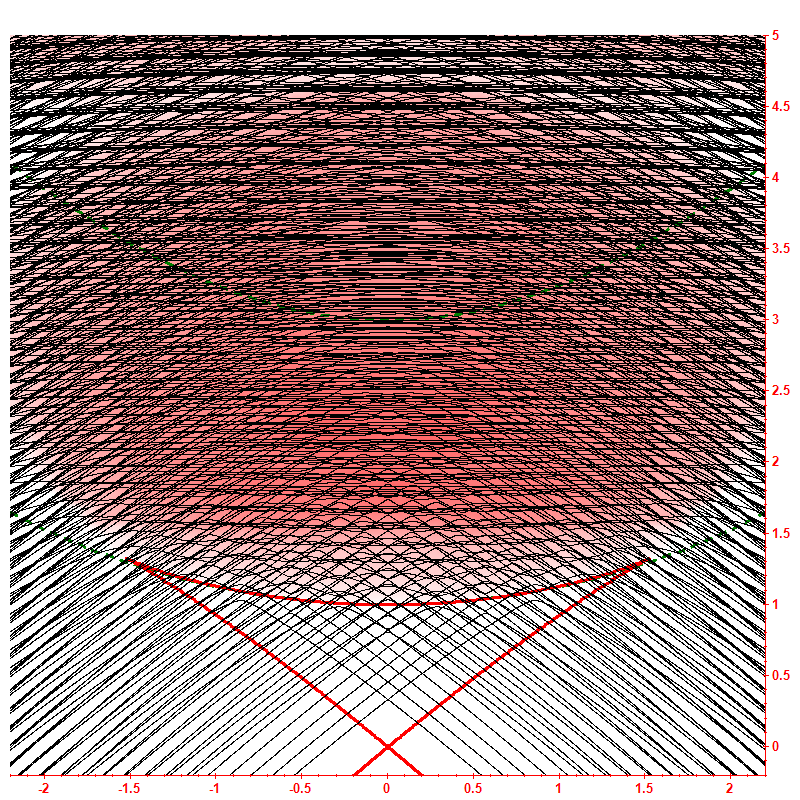
Obrázek 6. (A; E) Dynamika hladin.
Intenzita červené barvy v pozadí vyjadřuje klasickou chaoticitu (viz Obrázek 3).
Zelené čárkované čáry oddělují plně konvexní a částečně konkávní tvar hranice kinematicky dostupné oblasti.
Červené čáry odpovídají polohám stacionárních bodů potenciálu (kritický trojúhelník).
Zhlazená dynamika hladin (oscilující část hustoty hladin) se zobrazí po kliknutí na obrázek.		Obrázek 7. (x; E) Peresova mříž pro x=<x> (vodorovná osa) a E=<H> (svislá osa).
Zelené čárkované čáry oddělují plně konvexní a částečně konkávní tvar hranice kinematicky dostupné oblasti.
Červená čára odpovídá tvaru potenciálu V(x, y=0).
Modrá čára zobrazuje na vodorovné ose klasickou regularitu freg(E).